도형 넓이 공식+부피 공식 총정리.zip

2025-05-26
6:02 오후
42

“99%가 외우기만 했던
도형 공식들” 외우기 전에
‘왜’를 물어야 하는 이유?
.

그동안 도형의 공식은 그저 시험을 위한
지루한 암기 대상에 지나지 않았습니다.

그러나 한 걸음만 더 깊이 들어가 보면,
정사각형의 넓이를 구할 때
왜 변의 길이를 두 번 곱해야 하는지,
마름모는 왜 대각선을 서로 곱해 2로 나누는
같은 근본적인 질문과 마주하게 됩니다.

정사각형에서 원기둥에 이르는
다양한 도형 공식들이 단순한 암기가 아니라
명확한 수학적 원리와 논리적 사고의 산물임을깨닫게 되실 것입니다.

공식은 문제를 푸는 과정에서
자연스럽게 발견된 결과값입니다.
마치 퍼즐을 풀다 보면,
퍼즐 조각들이 맞춰지듯,

공식이란,
도형에 대한 깊은 이해 끝에 도달하는
일종의 알맹이 같은 것입니다.

그런데,
우리는 그 알맹이를 만들기 위한 과정은
건너뛴 채, 결과만 통째로
외워오고 있었던 셈입니다.

아이러니하게도,
원리를 모른 채 공식을 반복하는 일이
오히려 수학의 본질을 가장 멀리
돌아가게 만드는 길이었습니다.

하지만 그 본질을 다시 되짚고 나면,
막연히 어렵게만 느껴졌던 수학이
훨씬 명확해지고,
외워야만 한다고 여겼던 공식들도
오히려 당연하게 이해되는 구조로
보이기 시작하고 흥미도 생기게 됩니다.

이제, 도형 공식에 담긴 깊은 원리와
직관의 문을 함께 열어보시겠습니까?

평면도형 넓이 공식 총정리

정사각형 넓이 공식

한 변 × 한 변 = a × a = a²

이유: 넓이는 도형 안에 몇 개의 칸이 들어가는지를 세는 거예요.
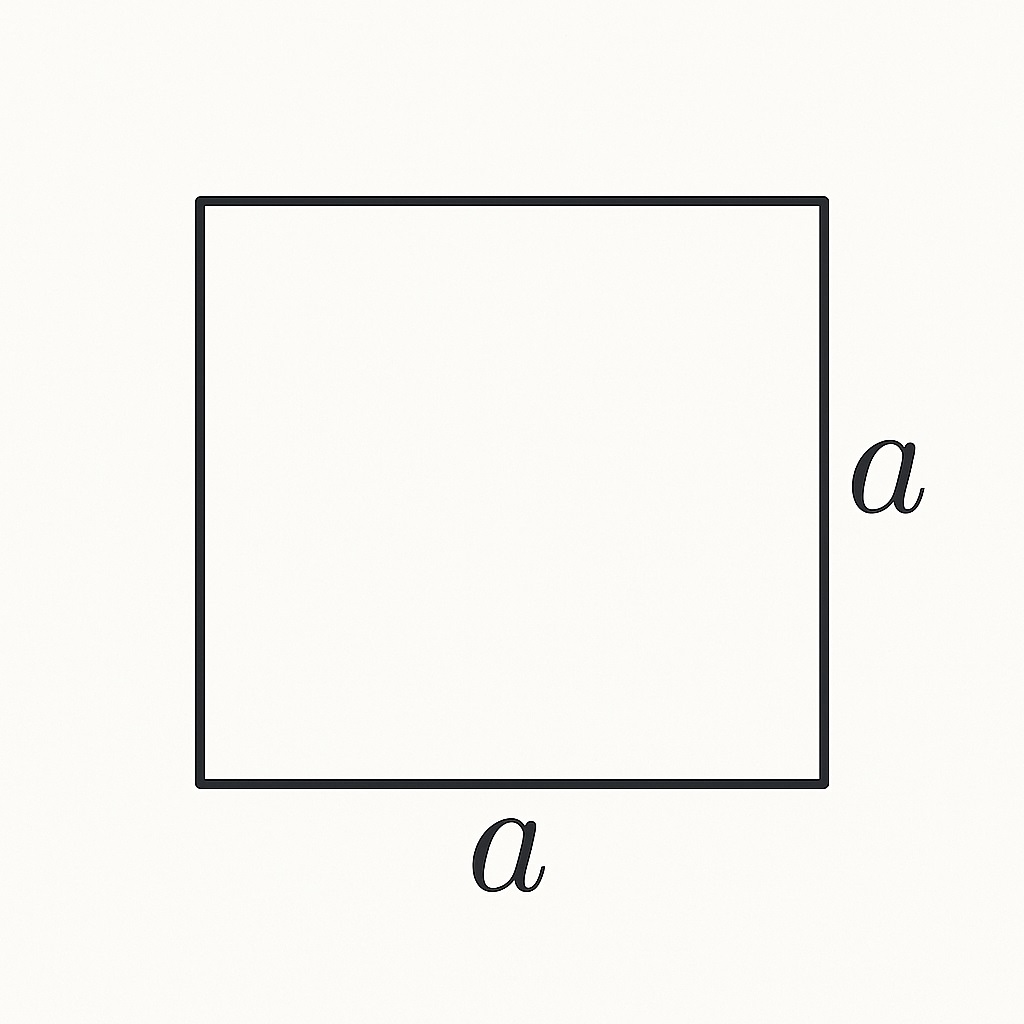
정사각형의 한 변이 a라면, 가로로 a개의 칸이 있고, 그런 줄이 아래로 a줄 있어요.
칸 하나하나가 1제곱단위라면, 전체 칸 개수는 가로 칸 수 × 줄 수, 즉 a × a가 됩니다.
그래서 a × a = a² 공식이 자연스럽게 도출되는 거예요.
▶ 왜 가로 × 세로인가요? 도형을 가장 작은 칸으로 나누면, 가로에 몇 개, 세로에 몇 줄이 들어가는지를 곱해야 전체 칸 수, 즉 넓이가 되기 때문이에요.

삼각형 넓이 공식

밑변 × 높이 ÷ 2

이유: 넓이를 구할 때는 보통 사각형처럼 ‘칸’으로 나눠서 생각하는데,
삼각형은 직사각형이나 평행사변형을 반으로 잘라서 만든 도형이에요.
그래서 넓이도 그 도형의 절반이 되는 거예요.
즉, 사각형의 넓이 공식인 가로 × 세로의 절반이니까,
밑변 × 높이 ÷ 2가 삼각형 넓이 공식이 되는 거예요.
▶ 왜 밑변 × 높이 ÷ 2인가요? 사각형을 반으로 자르면 삼각형이 되고, 넓이도 정확히 절반이 되기 때문이에요.

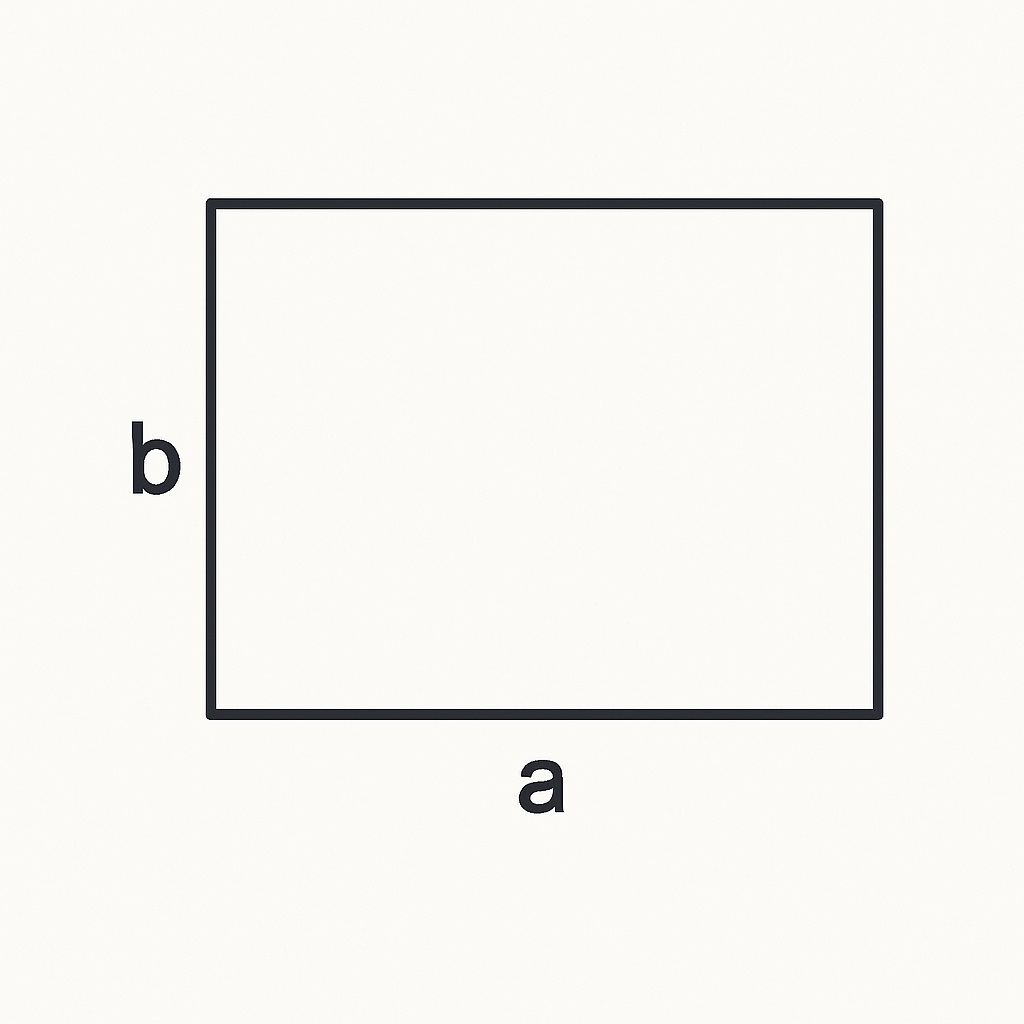
직사각형 넓이

가로 × 세로
= a × b

이유: 넓이는 도형 안에 몇 개의 칸이 들어가는지를 세는 거예요.
직사각형의 가로가 a칸이고 세로가 b줄이라면, 한 줄에 a칸이 있고 그런 줄이 b줄 있으니까 a × b칸이 있는 거예요.
그래서 넓이는 가로 × 세로 = a × b가 됩니다.
▶ 왜 가로 × 세로인가요? 도형을 가장 작은 칸으로 나누면, 가로에 몇 개, 세로에 몇 줄이 들어가는지를 곱해야 전체 칸 수, 즉 넓이가 되기 때문이에요.

마름모 넓이 공식

대각선₁ × 대각선₂ ÷ 2

이유: 마름모 안에는 두 개의 대각선이 있고, 이 대각선을 기준으로 자르면 네 개의 직각삼각형이 만들어져요.
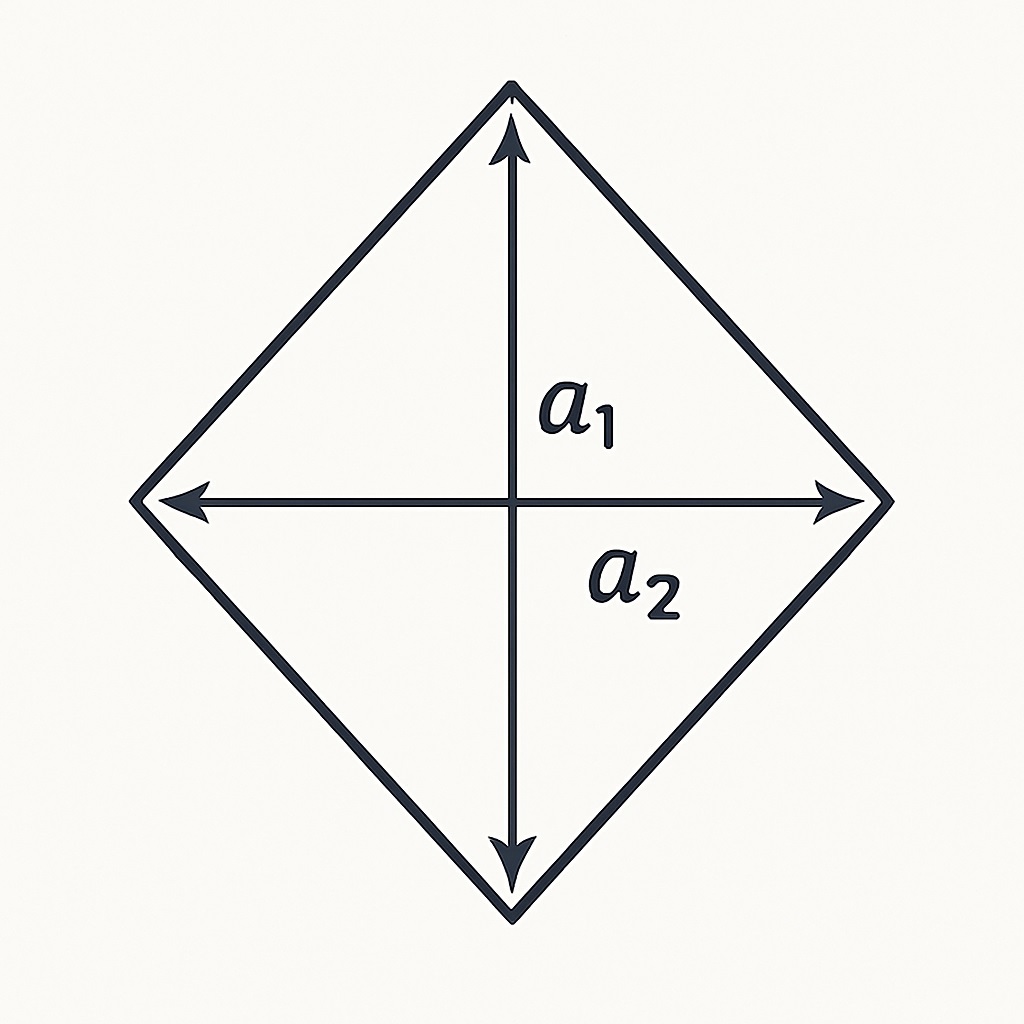
이 삼각형들을 재배치하면 사각형처럼 될 수 있기 때문에,
전체 넓이는 대각선₁ × 대각선₂의 절반이 되는 거예요.
그래서 마름모 넓이는 대각선₁ × 대각선₂ ÷ 2로 계산됩니다.
▶ 왜 대각선을 곱하고 2로 나누나요?
마름모는 대각선을 기준으로 삼각형 4개로 나눌 수 있고, 이 넓이를 합치면 전체 면적이 두 대각선의 곱의 절반이 되기 때문이에요.

사다리꼴 넓이 공식

(윗변 + 아랫변) × 높이 ÷ 2

이유: 사다리꼴을 세로로 잘라보면,
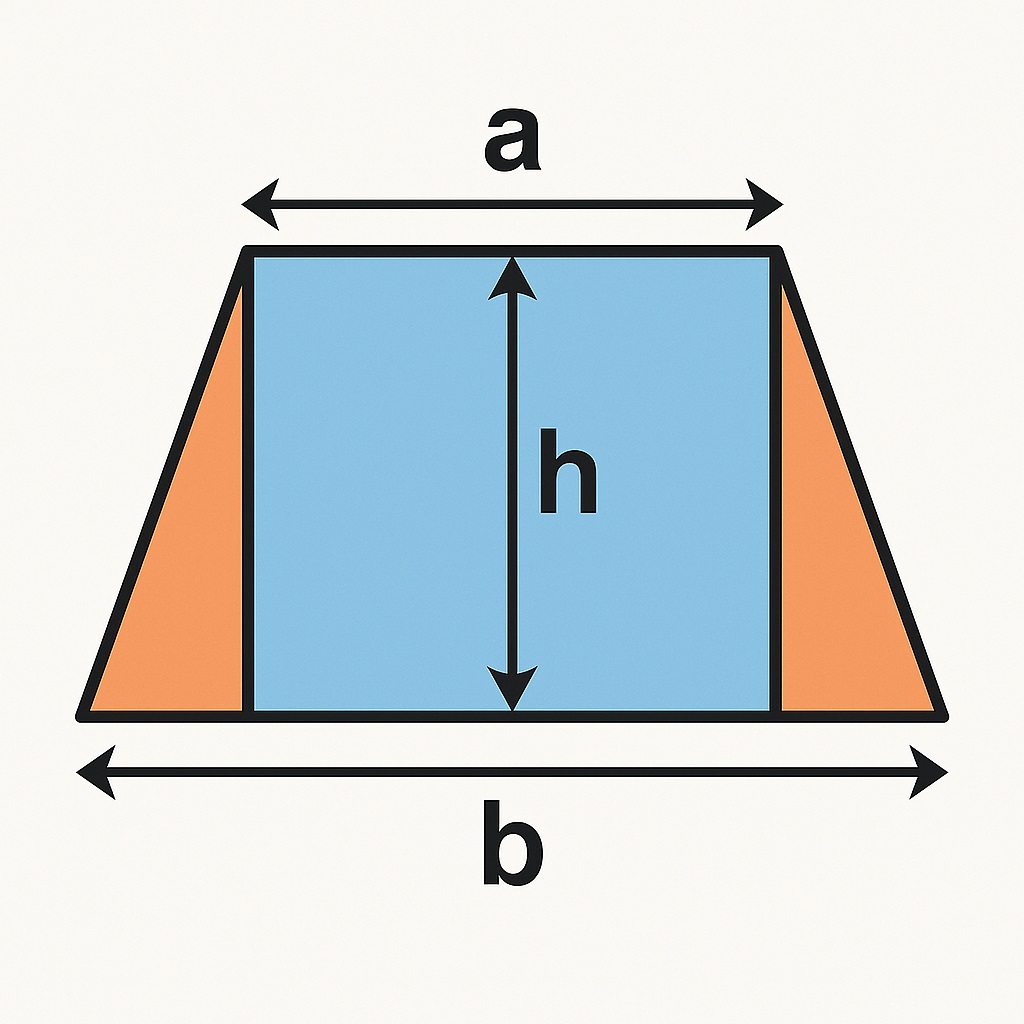
가운데는 직사각형이고, 양쪽에는 삼각형 두 개가 만들어집니다.

▶ 직사각형의 넓이 = 윗변 × 높이
▶ 양쪽 삼각형의 넓이 = (아랫변 − 윗변) × 높이 ÷ 2

이 둘을 더하면 전체 넓이는:
[윗변 × 높이] + [(아랫변 − 윗변) × 높이 ÷ 2]
→ 정리하면 (윗변 + 아랫변) × 높이 ÷ 2가 됩니다.

▶ 결론:
이 공식은 단순히 평균을 곱하는 게 아니라,
도형을 실제로 나눠서 각각의 넓이를 더한 결과로 만들어진 **진짜 수학적인 공식**입니다.

원의 넓이 공식

π × r²

이유: 원은 겉보기엔 단순하지만, 넓이를 구하는 과정은 아주 특별합니다.

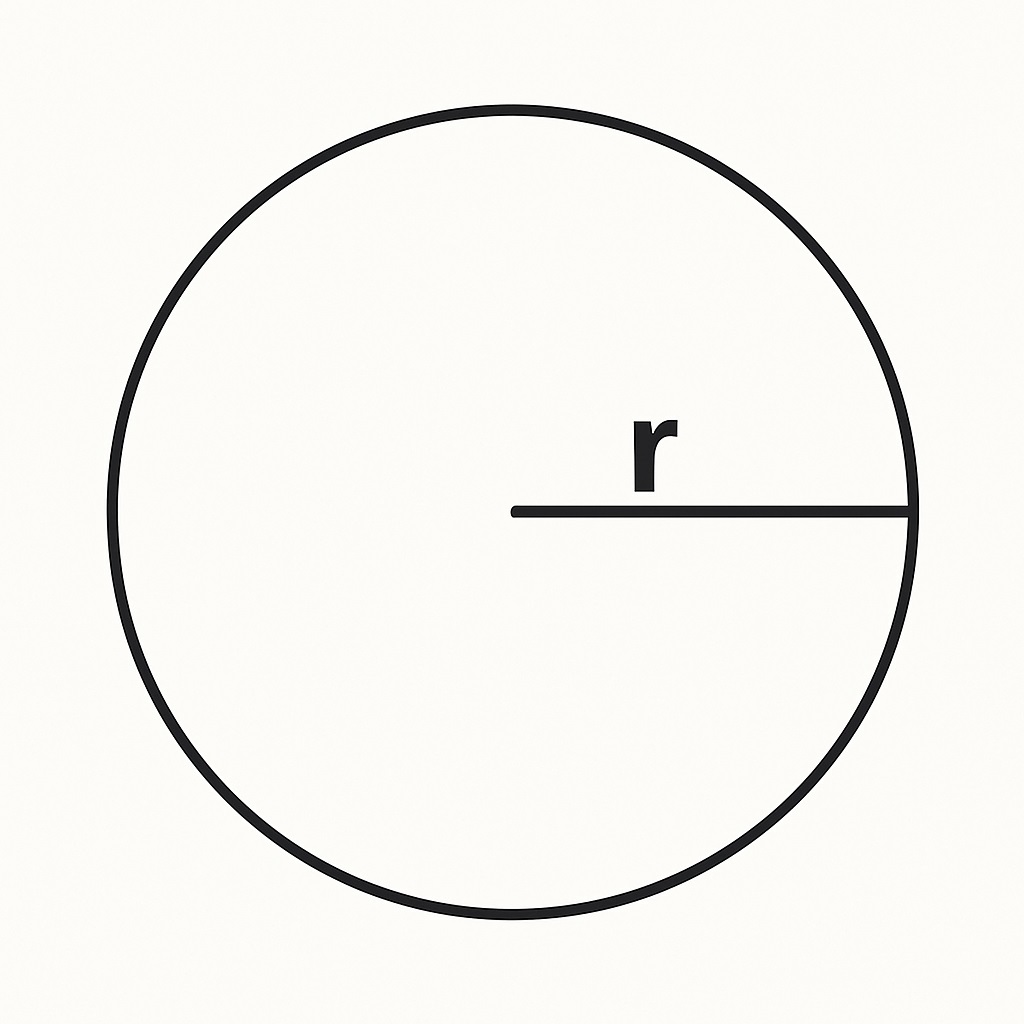
원을 아주 잘게 나누고 반으로 접어서 나열하면 거의 직사각형처럼 보이게 만들 수 있어요.

이때 직사각형의
▶ 가로 길이는 반지름 r
▶ 세로 길이는 반지름 r을 따라 생긴 호 길이 = π × r

그래서 넓이는 r × (π × r) = π × r²가 됩니다.

▶ π(파이)란?
파이는 **원둘레 ÷ 지름**의 값으로, 원의 둘레와 반지름 사이의 관계를 나타내는 **고정된 비율**입니다.
아무리 큰 원이든, 작은 원이든 π는 항상 약 3.14159로 일정해요.

부채꼴 넓이 공식

π × r² × (중심각 ÷ 360)

이유: 부채꼴은 원의 일부분이기 때문에, 원 전체 넓이인 π × r²에서 차지하는 각도의 비율만큼 곱해주면 됩니다.

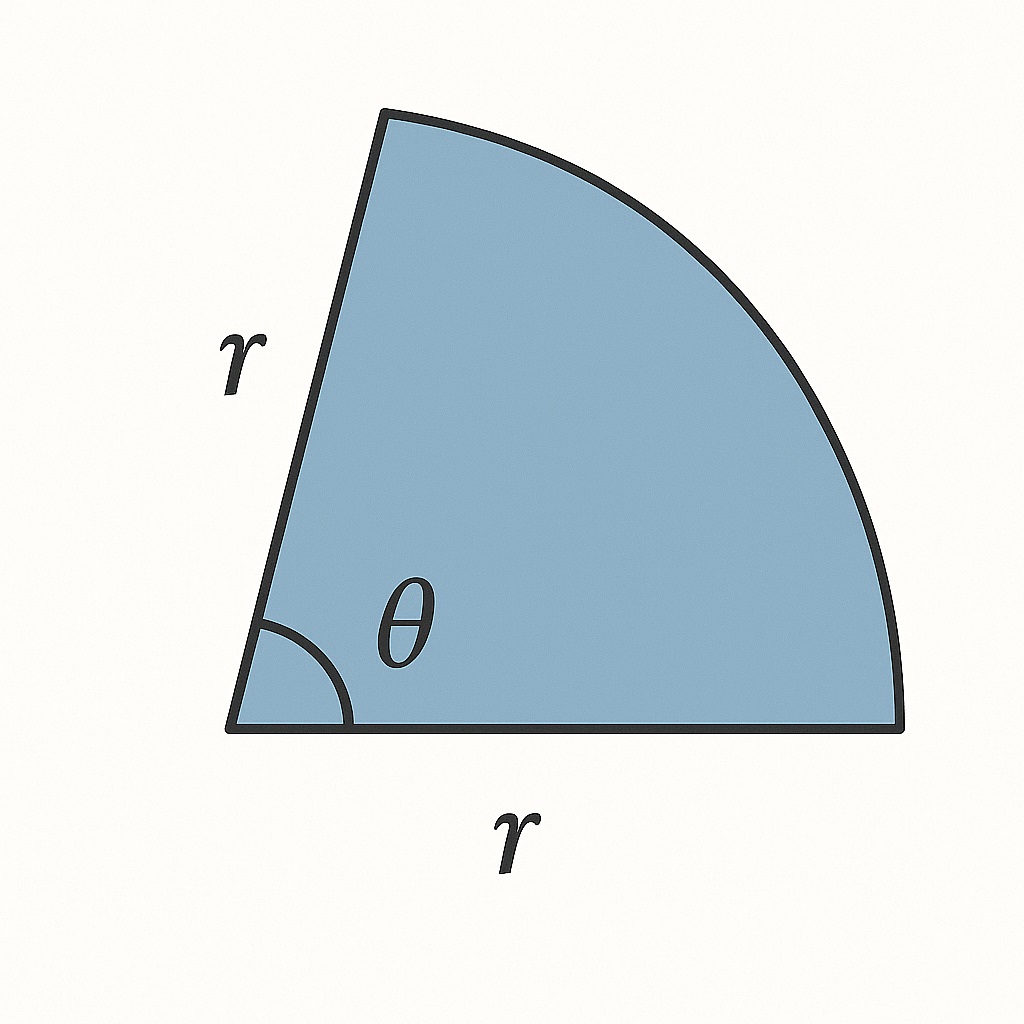
예를 들어 중심각이 90도라면,
원의 360도 중 90도를 차지하므로 전체 넓이의 ¼만 해당하겠죠?
→ π × r² × (90 ÷ 360) = 전체의 1/4 넓이

▶ 중심각이 중요한 이유?
중심각은 원에서 몇 도만큼 잘라냈는지를 의미해요.
부채꼴은 중심각의 크기에 따라 넓이가 정해지기 때문에, 항상 각도 ÷ 360의 비율을 곱해서 넓이를 구하는 거예요.

정팔각형 넓이 공식

2 × (1 + √2) × a²

이유:
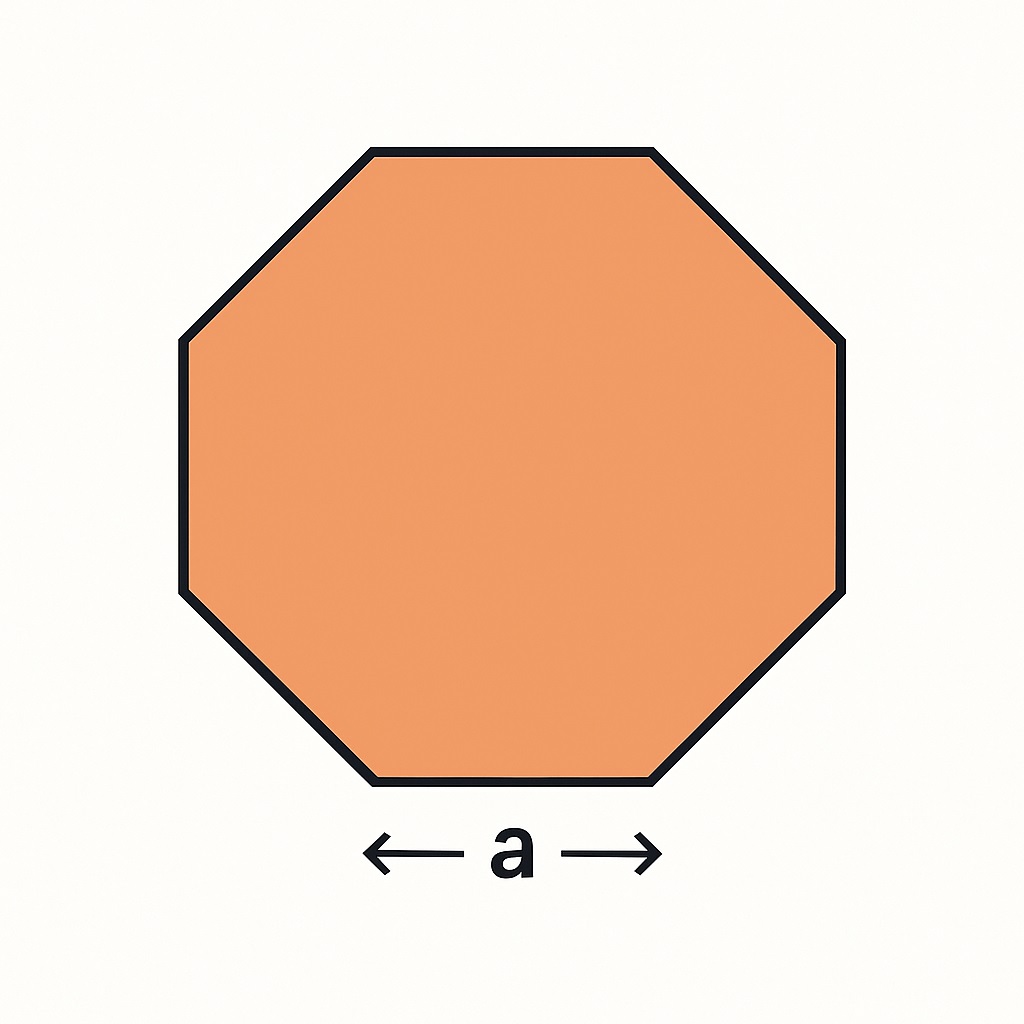
정팔각형은 **8개의 똑같은 이등변삼각형**으로 쪼갤 수 있어요.
중심에서 각 꼭짓점으로 선을 그으면, 정팔각형은 **8조각의 조각 피자**처럼 나뉘게 됩니다.

각 삼각형의 밑변은 한 변의 길이 `a`, 중심각은 45도(360° ÷ 8)이며, 삼각비 또는 피타고라스 정리를 이용해 이 삼각형 하나의 넓이를 계산할 수 있어요.

▶ 이 계산을 모두 정리하면 **하나당 넓이 = (1 + √2)/4 × a²**
▶ 여기에 삼각형이 8개니까 ×8
그래서 최종 공식은 2 × (1 + √2) × a²가 됩니다.

✔ 공식은 단순 외우는 게 아니라,
실제로 도형을 쪼개고, 각 조각의 구조와 수학 원리를 따라가 보면 자연스럽게 도출되는 결과입니다.

🧊 입체도형 부피 및 겉넓이 공식 정리

직육면체 부피 & 겉넓이 공식

📦 부피: 가로 × 세로 × 높이
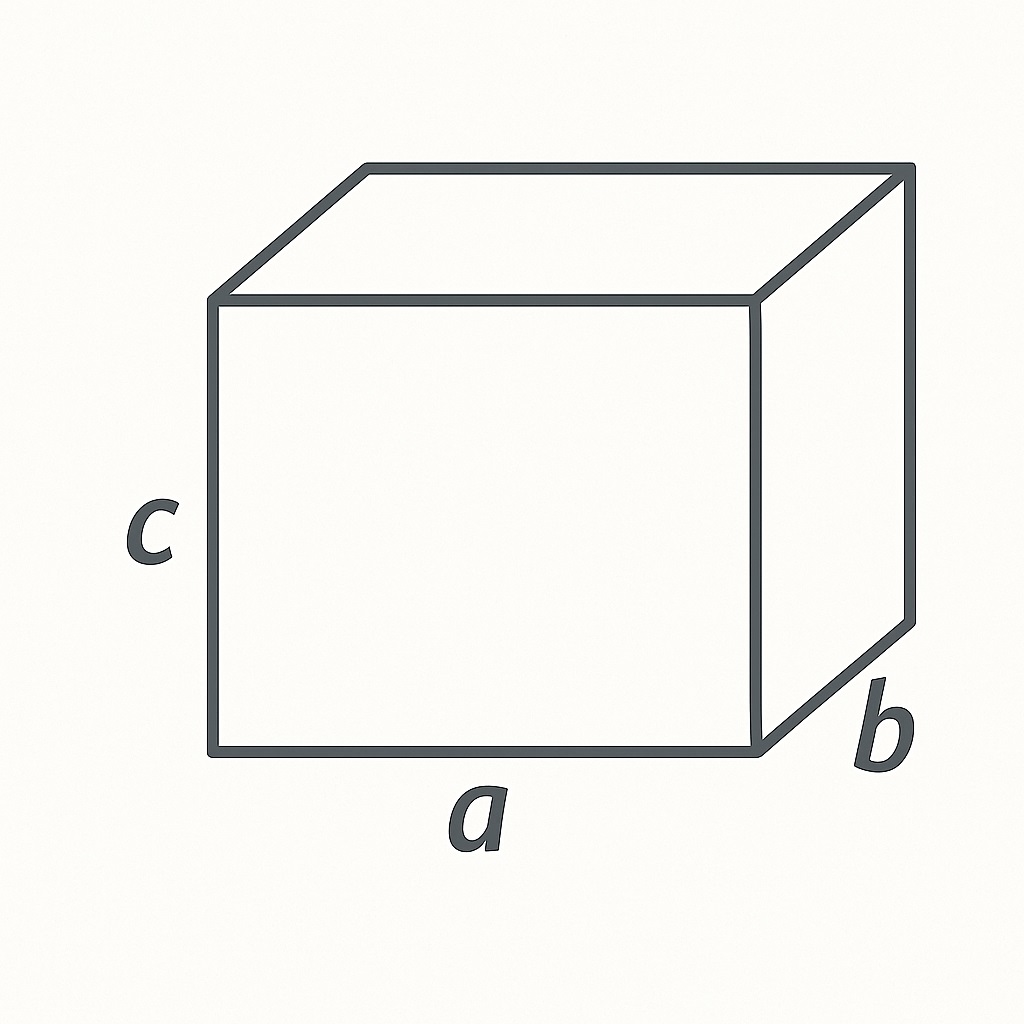
📏 겉넓이: 2 × (가로×세로 + 세로×높이 + 가로×높이)

📦 부피는 왜 가로 × 세로 × 높이인가요?
바닥 면적(가로 × 세로)에다가 위로 높이만큼 쌓는 구조입니다.
블럭을 바닥에 가로로 놓고, 그 위에 높이만큼 층을 쌓는다고 생각해보세요.
그래서 가로 × 세로 × 높이가 부피가 돼요.

📏 겉넓이는 왜 저렇게 구하나요?
직육면체에는 총 6개의 면이 있어요.
서로 마주보는 3쌍의 면이 **서로 같은 크기**예요:
● 앞/뒤: 가로 × 세로
● 왼쪽/오른쪽: 세로 × 높이
● 위/아래: 가로 × 높이

그래서 이 3쌍을 각각 2번 더하면:
2 × (가로×세로 + 세로×높이 + 가로×높이)가 됩니다.

📐 이렇게 생각하면 더 쉬워요!
직육면체를 종이 상자처럼 **완전히 펼쳤다고 생각**해보세요.
그러면 6개의 면이 평면 위에 전개도처럼 나열되죠?
그 각각의 면의 넓이를 구해서 다 더한 값이 곧 **겉넓이**가 되는 거예요.

📦

정육면체 부피 & 겉넓이 공식

부피: a³
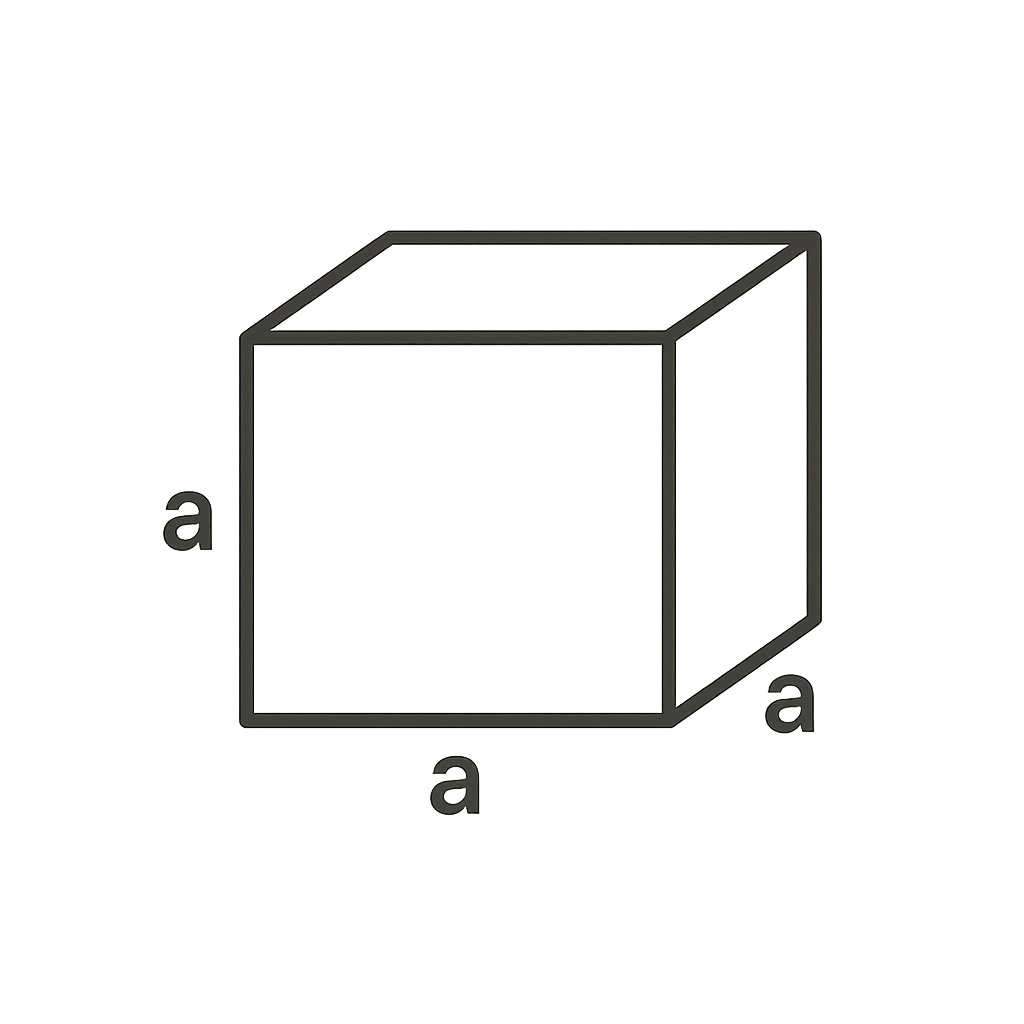
겉넓이: 6a²

📦 부피 공식 (a³):
정육면체는 정사각형 면 6개로 이루어진 도형이에요.
가로, 세로, 높이가 모두 a이기 때문에 a × a × a = a³이 부피가 됩니다.

📏 겉넓이 공식 (6a²):
정육면체는 **정사각형 6개**로 이루어져 있고, 각 면의 넓이는 a × a = a²입니다.
이 면이 6개 있으니까
6a²가 전체 겉넓이가 되는 거예요.

📐 참고:
종이로 정육면체 상자를 만든다고 생각해보면, 같은 정사각형 6장을 붙이면 딱 맞게 만들어지죠? 그 구조를 그대로 공식으로 표현한 겁니다.

원기둥 부피 & 겉넓이 공식

부피: π × r² × h
겉넓이: 2πr² + 2πrh

📦 부피 공식 (π × r² × h):
원기둥은 원이 위로 높이만큼 쌓인 구조입니다.
밑면의 넓이 (π × r²)에다가 높이 h만큼 층을 쌓으면
π × r² × h가 부피가 돼요.

📏 겉넓이 공식 (2πr² + 2πrh):
● 윗면과 아랫면은 반지름 r인 원 2개 → 2πr²
● 옆면은 원기둥을 옆으로 펼치면 **직사각형이 되는데**, 이 직사각형의 가로는 원의 둘레 (2πr), 세로는 높이 h
그래서 옆면 넓이는 2πr × h = 2πrh

→ 전체 겉넓이 = 2πr² + 2πrh

원뿔 부피 & 겉넓이 공식

부피: ⅓ × π × r² × h (아르키메데스 발견)
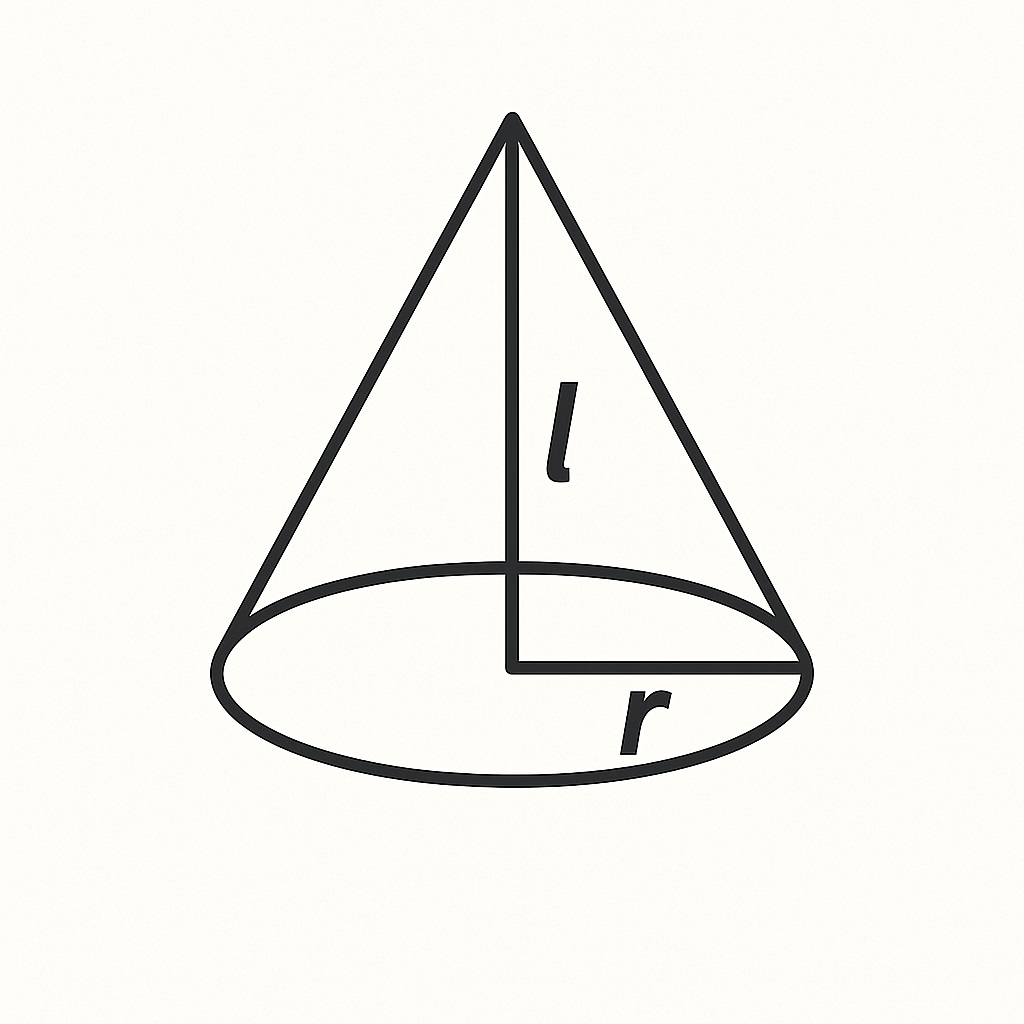
겉넓이: πr² + πrl

📦 부피 공식 (⅓ × π × r² × h):
원뿔은 원기둥의 3분의 1 구조예요.
밑면의 넓이 (π × r²)에다가 높이 h만큼 층을 쌓되,
점점 좁아지며 쌓이기 때문에 1/3 계수가 붙어요.

이 관계는 고대 그리스 수학자 아르키메데스가 처음 증명했습니다.
그는 같은 밑면과 높이의 원기둥과 원뿔, 구의 부피를 비교하며 이 ⅓ 관계를 기하학적으로 증명했어요.

📏 겉넓이 공식 (πr² + πrl):
● 밑면 원의 넓이: πr²
● 옆면 곡면은 부채꼴 모양으로 펴졌을 때 → π × r × l (l은 모선)
→ 전체 겉넓이 = πr² + πrl

구의 부피 & 겉넓이 공식

부피: ⅘ × π × r³ (아르키메데스 증명)
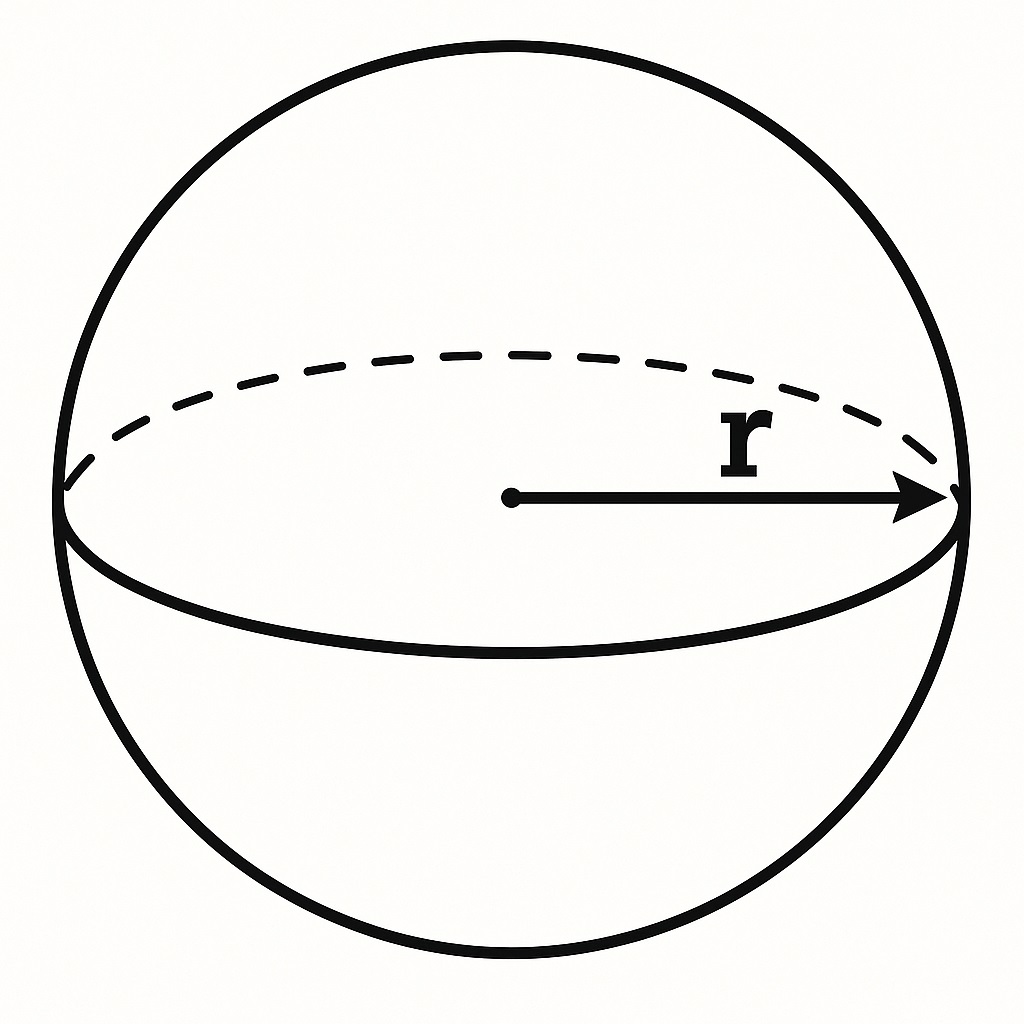
겉넓이: 4πr² (고대 최초 증명)

📦 부피 공식 (⅘ × π × r³):
구는 3차원 공간을 가득 채운 완전한 곡면 도형입니다.
반지름 r을 기준으로 모든 방향에 균일하게 퍼져 있기 때문에 r³이 등장하고, 고대 그리스의 수학자 아르키메데스는 『구와 원기둥에 관하여 (On the Sphere and Cylinder)』라는 책에서 그 부피가 원기둥의 2/3임을 처음 증명하며 \(\frac{4}{3}πr³\) 공식을 도출했어요.

📏 겉넓이 공식 (4πr²):
구의 표면 전체는 **같은 반지름을 가진 원의 넓이(πr²)** 4개와 같아요.
이를 이용해 4πr²이라는 공식이 유도됩니다.
아르키메데스는 이 겉넓이 공식도 함께 증명했으며, 이 공식은 이후 수천 년간 그대로 사용되고 있어요.

🧠 역사 포인트:
아르키메데스는 이 사실을 너무 자랑스러워해 본인의 무덤 비문에 “구가 내접한 원기둥”을 새겨달라고 유언까지 남겼어요.